Առաջադրանք 1․ Գտել ենթական և ուղիղ խնդիրը։
Մեսրոպ Մաշտոցն ստեղծեց հայոց գրերը։
Տղան միայնակ վերանորոգեց տունը։
Երեխան ջանասիրաբար գիրք է կարդում :
Հեքիաթները հորինում են մարդիկ ` կյանքի տխրությունը ցրելու համար։
Նա սիրում է մայրիկին։
Առաջադրանք 2․ Գտնել հանգման անուղղակի խնդիրները։
Զբոսաշրջիկները մոտեցան եկեղեցուն։
Երեխան հավատում էր մոր խոսքին։
Ծեր կինն աղոթում էր Աստծուն։
Փողոցով քայլելիս ժպտում էր բոլորին։
Առաջադրանք 3․
Գտիր նախադասությունների ենթական, ստորոգյալը, ուղիղ խնդիրը և հանգման խնդիրը։
Աշակերտը մի անգամ հարց ուղղեց վարպետին։
Կարճ ժամանակում նա վաճառեց ապրանքը անգլիացիներին:
Դասղեկը գիրքը հանձնեց երեխային:
Իմ մտքում հրաժեշտի խոսքեր եմ ասում հին քաղաքին, իմ ընկեր Անդոյին։
Աստված Մովսեսին պատվիրում է մոլորյալ ժողովրդին դարձի բերել:
Պատասխաններ
Առաջադրանք 1․ Գտել ենթական և ուղիղ խնդիրը։
Մեսրոպ Մաշտոցն ստեղծեց հայոց գրերը։
Տղան միայնակ վերանորոգեց տունը։
Երեխան ջանասիրաբար գիրք է կարդում :
Հեքիաթները հորինում են մարդիկ ` կյանքի տխրությունը ցրելու համար։
Նա սիրում է մայրիկին։
Առաջադրանք 2․ Գտնել հանգման անուղղակի խնդիրները։
Զբոսաշրջիկները մոտեցան եկեղեցուն։
Երեխան հավատում էր մոր խոսքին։
Ծեր կինն աղոթում էր Աստծուն։
Փողոցով քայլելիս ժպտում էր բոլորին։
Առաջադրանք 3․
Գտիր նախադասությունների ենթական, ստորոգյալը, ուղիղ խնդիրը և հանգման խնդիրը։
Աշակերտը մի անգամ հարց ուղղեց վարպետին։Ենթակա-աշակերտ,ստորոգյալ-ուղղեց,հանգման խնդիր-վարպետին,ուղիղ խնդիր-հարց
Կարճ ժամանակում նա վաճառեց ապրանքը անգլիացիներին:Ենթակա-նա,ստորոգյալ-վաճառեց,ուղիղ խնդիր-ապրանք․հանգման խնդիր-անգլիացիներ
Դասղեկը գիրքը հանձնեց երեխային:Ենթակա-դասղեկը,ստորոգյալ-հանձնեց,ուղիղ խնդիր-գիրքը․հանգման խնդիր-երեխային
Իմ մտքում հրաժեշտի խոսքեր եմ ասում հին քաղաքին, իմ ընկեր Անդոյին։Ենթակա-Իմ,ստորոգյալ-ասում,ուղիղ խնդիր-հրաժեշտ,հանգման խնդիր-Անդոյին
Աստված Մովսեսին պատվիրում է մոլորյալ ժողովրդին դարձի բերել:Ենթակա-Աստված,ստորոգյալ-պատվիրում է,ուղիղ խնդիր-ժողովրդին,հանգման խնդիր-Մովսեսին
Category: Մաթեմատիկա
Երկրաչափություն 16.12.2022
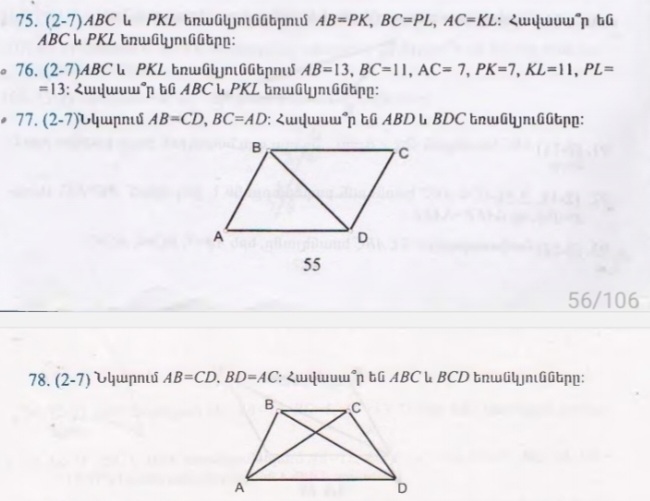
75.Ըստ Երորդ հայտանիշի ABC=PKL
76.Ըստ Երորդ հայտանիշի
77AB=CD BC=AC DB ընդանուր Ըստ Երորդ հայտանիշի ԵրանկունԵրը հավսարԵն
Դաս 3.
Դաս 3.
Կրկնենք անցածը
Առաջադրանքներ(դասարանում)
1) Գրե՛ք երեք հաջորդական ամբողջ թվեր, որոնց գումարը հավասար
է 0-ի։-1+0+1
2) Հաշվել.
ա)( -44:4+12:(-3))-134=-149
բ) -12+(-34)-(-21)=-25
գ) -34+6-91=-118
դ) -(-56)-(-21)+100=+177
ե)-120:2+60=0
3) AB հատվածը C կետով բաժանվում է AC և CB երկու հատվածների։
CB հատվածի երկարությունը AC հատվածի երկարության 23-ն է։
Գտե՛ք AB հատվածի երկարությունը, եթե CB հատվածի երկարությունը 24 սմ է։1)1մասը=24:2=12 2)AC=3×12=36 3)AB=36+24=64 մաս
4) Արույրը 60 % պղնձի և 40 % ցինկի համաձուլվածք է։ Արույր պատրաստելու համար վառարանի մեջ դրել են ցինկ և 210 կգ պղինձ։
Որքա՞ն ցինկ են դրել վառարանի մեջ։ Որքա՞ն արույր կստացվի։1)210:3=70 2)2×70=140 3)210+140=350
Լրացուցիչ(տանը)
5) Գտե՛ք արտահայտության արժեքը.
ա) (35 – 17) – 20, դ) (29 – 64) + 23, է) (–39 –21) + 11
բ) (–43 – 14) – 32, ե) (–30 – 21) + 56, ը) (16 – 33) – 50,
գ) (–74 + 27) – 15, զ) (81 – 45) – 60, թ) (–18 + 6) – 39:
6) Հաշվե՛ք.
ա) | – 4 – *|, եթե աստղանիշի փոխարեն գրված լինի –3 թիվը,
բ) |5 – * – 8|, եթե աստղանիշի փոխարեն գրվի –9 թիվը,
գ) |* – 2| + |* – (–1)|, եթե աստղանիշի փոխարեն գրվի 6 թիվը։
7) Քաղաքից դուրս եկավ մի մեքենա, որի արագությունը 80 կմ/ժ էր։
հետո նրա հետևից շարժվեց մեկ ուրիշ մեքենա, որի արագությունը
90 կմ/ժ էր։ Քաղաքից դուրս գալուց ինչքա՞ն ժամանակ անց
երկրորդ մեքենան առաջինից 20 կմ առաջ անցած կլինի։
8) Գտնել բաց թողած թիվը.
11
Դաս 3.
Դաս 3.
2. Ամբողջ թվերի շարքը և ամբողջ թվերի համեմատումը
Տեսական նյութ
Մենք գիտենք, որ բնական (դրական ամբողջ) թվերի շարքն այնպես
է կազմված, որ նրա յուրաքանչյուր թիվ ստացվում է` նախորդ թվին
(սկսած 1-ից) 1 գումարելով.
1, 2, 3, 4, 5, 6 …
Ուրեմն համեմատման նշանների միջոցով կարող ենք գրել.
0 < 1 < 2 < 3 < 4 < 5 < 6 …
Այժմ հիշենք, որ յուրաքանչյուր բացասական ամբողջ թիվ ստացվում է` նախորդից (սկսած –1-ից) 1 հանելով:Այսպիսով` ստանում
ենք բացասական ամբողջ թվերի շարքը.
… –6, –5, –4, –3, –2, –1։
Այս շարքում յուրաքանչյուր հաջորդ թիվ 1-ով փոքր է նախորդից։
Այսպիսով`
… < –6 < –5 < –4 < –3 < –2 < –1 < 0։
Միավորելով դրական և բացասական ամբողջ թվերի շարքերը և
0-ն` ստանում ենք ամբողջ թվերի շարքը.
… – 6, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6 …
Կարելի է տեսնել, որ ամբողջ թվերի շարքում յուրաքանչյուր թիվ
մեծ է իրենից ձախ գրված ցանկացած թվից և փոքր է իրենից աջ
գրված ցանկացած թվից.
… < –6 < –5 < –4 < –3 < –2 < –1 < 0 < 1 < 2 < 3 < 4 < 5 < 6 < …
Ամբողջ թվերի շարքը, ի տարբերություն բնական թվերի շարքի,
երկու կողմից էլ անվերջ է. չկա ինչպես ամենամեծ, այնպես էլ
ամենափոքր ամբողջ թիվ։
Առաջադրանքներ(դասարանում)
1) Երկու ամբողջ թվերից ո՞րն է ավելի մեծ.
ա) դրակա՞ն թիվը, թե՞ զրոն,դրական
բ) բացասակա՞ն թիվը, թե՞ զրոն,զրոն
գ) դրակա՞ն թիվը, թե՞ բացասական։դրական
2) x թիվը դրակա՞ն է, թե՞ բացասական, եթե`
ա) x > 0, բ) x < 0:ա)դրական բ)բացասական
3) Համեմատե՛ք ամբողջ թվերը.
ա) 0 > –3, դ) –1 < 1, է) –13 < 2,
բ) –4 < 2, ե) 5 > –3, ը) –1000 < 1,
գ) –3 < –10, զ) –16 < –12, թ) 25 > –25։
4) Գրե՛ք որևէ յոթ ամբողջ թվեր, որոնք փոքր են՝
ա) 4-ից,-5,-6,-7 գ) 6-ից,-7 ե) –5-ից, -6,-7է) 3-ից-4,-5,-6,-7
բ) 0-ից, -1,-2,-3,-4,-5,-6,-7դ) –1-ից-2,-3,-4,-5,-6,-7 զ) –10-ից,-11,-12-,13-,-14,-15,-16,-17 ը) –3-4,-5,-6,-7ից։
Առաջադրանքներ(տանը)
5) Գրե՛ք հետևյալ թվերը`
ա) աճման կարգով. 31-32,33,34,35…, –1—2,-3,-4,-5,-6,-7…, – 7,—8,-9,-10…,–1,-2,-3,-4,-5,… 0, -1,2,3,4…,–11,—12,-13…, 24—25,25,27…, 7, -8,9,10…,– 2,-3,-4,-5.. ,–6,-7,-9,-10…
բ) նվազման կարգով. –11,-12,-13…, –3,-4,-5…, –7,—8,-9,-10…, 12,-12,13,14.., 4,5,6,7,8…, –8,-9,-10…, –17,—18,-19-20…, –30,-31,-32,-33…, 1,2,3,4,5…, 0,1,2,3…, 13,14,15,…։
6) Գտե՛ք այն բոլոր ամբողջ արժեքները, որոնք աստղանիշի
փոխարեն գրելու դեպքում կստացվի ճիշտ անհավասարություն.
ա) 0 < 1 < 3, գ) –4 < -5< 3, ե) –14 < -15 < –5,
բ) –4 < -5 < 0, դ) –5 < -6 < 5, զ) –28 < -29 < –22։
7) Գրի՛ առեք հետևյալ պնդումները՝ օգտագործելով անհավասարու-
թյունների նշանները.
ա) 11-ը մեծ է 0-ից, գ) –10-ը բացասական թիվ է,
բ) –7-ը փոքր է 0-ից, դ) 2-ը դրական թիվ է։
8) Գրե՛ք որևէ յոթ ամբողջ թվեր, որոնք մեծ են՝
ա) –3-ից,4,5,6,7 գ) –7-ից,- 5,6,7ե) 2-ից,3,4,5,6,7 է) –56,7,8-ից,
բ) –6-ից, 7դ) 0-ից,1,2,3,4,5,6,7 զ) 10-ից, 5,6,7ը) 5-ից6,7։
Լրացուցիչ
Խնդրագրքից—խնդիր 1-ի 1-ից 10-ը,էջ 22,Շարժման խնդիրներ։
5) 500 կգ հանքաքարից ստացել են 77 կգ պղինձ։ Ինչքա՞ն պղինձ
կստացվի 300 կգ հանքաքարից։300×77=23000 23000:500=46.2
6) Ստուգողական աշխատանքից անբավարար գնահատական է ստացել 14 աշակերտ: Անբավարար գնահատական ստացածների քանակը հարաբերում է դրական գնահատական ստացածների քանակին, ինչպես 2 ։ 7։ Քանի՞ աշակերտ է դրական գնահատական ստացել։x=14:2/7=14/1×7/2=7/1×7/1=49/1
7) 160 գ ծովի ջրում պարունակվում է 8 գ աղ։ Քանի՞ գրամ ծովի ջուրն
է պարունակում 56 գ աղ։ 160:8=20 20×56=1120
8) Բանվորը 8 ժ աշխատելու համար ստանում է 2500 դրամ։ Քանի՞
դրամ կստանա բանվորը 12 ժ աշխատելու համար։8*x=(12×2500)x=(12×2500):8=3750
9) Մետաղյա խորանարդը, որի կողի երկարությունը 13 սմ է, ունի 1352 գ զանգված։ Որքա՞ն է նույն մետաղից պատրաստված և 2 սմ կողով խորանարդի զանգվածը։x=2/1:13/1352=2/1×1352/13=2704/13 2704;13=208
Դաս 2 09.09.2021
2. Հարաբերություններ
Տեսական նյութ
Մաթեմատիկական տեսակետից՝ հարաբերությունը երկու թվերի քանորդն է. բաժանելին կոչվում է հարաբերության նախորդ անդամ, բաժանարարը՝ հարաբերության հաջորդ անդամ, իսկ քանորդը՝ հարաբերություն։
Հարաբերությունը ցույց է տալիս, թե քանի անգամ է հարաբերության
նախորդ անդամը մեծ հաջորդ անդամից կամ նրա որ մասն է։
Դիտարկենք մի օրինակ։
ABCD քառանկյան մակերեսը 6 սմ2 է, իսկ ABC եռանկյան մակերեսը՝
4 սմ2։ Քանի՞ անգամ է ABCD քառանկյան մակերեսը մեծ ABC եռանկյան մակերեսից, ABC եռանկյան մակերեսը ABCD քառանկյան մակերեսի ո՞ր մասն է։
Խնդիրը լուծելու համար պետք է կազմել 6 և 4, ինչպես նաև 4 և 6
թվերի հարաբերությունները։ Ունենք.
6:4=64=32, 4:6=46=23
Ստացված հարաբերությունները ցույց են տալիս, որ ABCD
քառանկյան մակերեսը 32 անգամ մեծ է ABC եռանկյան մակերեսից,
իսկ վերջինս ABCD քառանկյան մակերեսի 23-ն է։
Առաջադրանքներ
1) Ի՞նչ է հարաբերությունը, ինչպե՞ս են կոչվում հարաբերության անդամները:
2) Գտե՛ք հարաբերությունը.
ա) 3-ի և 5-ի, 3:5=3/5
բ) 6-ի և 32-ի, 6:32 =6/32
գ) 43-ի և 8-ի,43:8 =43/8
դ) 12-ի և 35-ի:12:35=12/35
3) ABC եռանկյան պարագիծը 64 սմ է, իսկ DEF եռանկյանը՝ 36 սմ։
Գտե՛ք ABC եռանկյան պարագծի հարաբերությունը DEF եռանկյան
պարագծին։ Ի՞նչ է ցույց տալիս այդ հարաբերությունը։ 64:36=64/36=16/9
4) 50 կգ կարմիր ներկն արժե 75000 դրամ, իսկ 85 կգ սպիտակ ներկը՝
123250 դրամ։ Ո՞ր ներկի գինն է ավելի բարձր։ 7500:50=1500 123250:85=1450
Լրացուցիչ առաջադրանքներ
5) Ռուս մաթեմատիկոս Պ. Լ. Չեբիշևը (1821-1894) ապացուցել է, որ 1-ից մեծ ցանկացած բնական թվի և նրանից երկու անգամ մեծ թվի միջև միշտ կա առնվազն մեկ պարզ թիվ։ Ստուգե՛ք Չեբիշևի պնդումը 9,15, 27 թվերի համար։ 9-15 դրանց միջ և պարզ թվերն են 11,13, 15 -30 պարզ թվերն են է 17 19 21 23 29 27-40 պարզ թվերն են 29 31 35 37 39
6) Գերանը սղոցով կտրելն արժե 50 դրամ: Ինչքա՞ն է պետք վճարել
գերանը 6 մասի բաժանելու համար:50×6=300
Մաթեմ
1․ Կատարի՛ր բաժանում, ապա ստուգիր ճիշտ ես կատարել այն։
Օրինակ՝
835:4=208(3 մն.)
| — | 8 | 3 | 5 | Ստուգում՝ | |||||||||
| 8 | 0 | 8 | 208×4+3=832+3=835 | ||||||||||
| — | 3 | 5 | |||||||||||
| 3 | 2 | ||||||||||||
974:9=18(մ2)
| — | 9 | 7 | 4 | Ստուգում՝ | |||||||||
| 9 | 8 | ||||||||||||
| — | 7 | 4 | |||||||||||
| 7 | 2 | ||||||||||||
740:13=56(մ12)
| — | 7 | 4 | 0 | 3 | Ստուգում՝ | ||||||||
| 6 | 5 | 6 | |||||||||||
| — | 9 | 0 | |||||||||||
| 7 | 8 | ||||||||||||
| 1 | |||||||||||||
5437:66= 82(մ25)
| — | 5 | 4 | 3 | 7 | 6 | Ստուգում՝ | |||||||
| 528 | 2 | ||||||||||||
| — | 1 | 5 | 7 | ||||||||||
| 1 | 3 | 2 | |||||||||||
| 5 | |||||||||||||
2․Լրացրե՛ք աղյուսակը․
| Բաժանելի | 593 | 845 | 7160 | 1372 | 2850 |
| Բաժանարար | 35 | 64 | 49 | 100 | 57 |
| Թերի քանորդ | 16 | 13 | 146 | 14 | 50 |
| Մնացորդ | 33 | 13 | 12 | 70 | 6 |
3․ Գտի՛ր․
- Գտիր 6257 թիվը 10-ի բաժանելիս ստացվող մնացորդը։625,7 մ
- Գտիր 537 թիվը 100-ի բաժանելիս ստացվող մնացորդը։537մ
- Գտի՛ր 4639 թիվը 10-ի բաժանելիս ստացված մնացորդը:463,9
- Գտի՛ր 3189 թիվը 100-ի բաժանելիս ստացված մնացորդը:31,89
- Գտի՛ր 2639 թիվը 1000-ի բաժանելիս ստացված մնացորդը:2,639
- Գտիր 8529 թիվը 10-ի բաժանելիս ստացված մնացորդը։852,9
- Գտիր 85449 թիվը 100-ի բաժանելիս ստացված մնացորդը։854,49
- Գտիր 8369 թիվը 1000-ի բաժանելիս ստացված մնացորդը։8,369
4. Լարի առաջին կտորը երկրորդից երկար է 6 անգամ, իսկ երկրորդ կտորը երրորդից կարճ է 4 անգամ։ Որքա՞ն է այդ լարերի երկարությունների գումարը, եթե երրորդ լարի երկարությունը 96մ է։
Լուծում
1)96:4=24
2)24×6=144
3)96+24+144=264
Պատ՝264
5. Ձեթը պահվում էր 2լ, 3լ և 6լ տարողությամբ անոթներում, ընդ որում վեցլիտրանոց անոթների քանակը 4 անգամ ավելի էր, քան երկուլիտրանոցներինը, և 2 անգամ ավելի, քան երեքլիտրանոցներինը։ Ընդամենը որքա՞ն ձեթ կար, եթե վեցլիտրանոց անոթներում եղած ձեթը 48լ էր։
Լուծում
1)48:4=12
2)48:2=24
3)48+12+24=84
Պատ՝84
6․ Առաջին տուփում կար 103 կոճակ, երկրորդում՝ 97, երրորդում՝ 89։ Առաջին տուփից երկրորդի մեջ դրեցին 36 կոճակ, երկրորդից երրորդի մեջ՝ 22, երրորդից առաջինի մեջ՝ 21։ Դրանից հետո ամենաշատ կոճակներ պարունակող տուփում քանի՞ կոճակով ավելի եղավ, քան ամենաքիչ կոճակներ պարունակողում։
Լուծում
1)103-36=67
2)97+36=133
3)133-22=111
4)89+22=111
5)111-21=90
6)67+21=88
Մաթեմ
Վարժ625
7:7=1
14:7=2
21:7=3
35:7=5
28:7=4
Վարժ588
37:10=3 .7
370:10=37
548:10=54.8
279:100=2.79
380:=3.80
2200:100=22
Վարժ589
245:10=24.5
2415:100=24.15
24150:1000=24.150
Վարժ651
3+3=6
124+6=130
130բազմապատիկե 10
Վարժ656
5:5=1
10:5=2
15:5=3
20:5=4
25:5=5
30:5=5
35:5=6
40:5=8
45:5=9
50:5=10
100:5=20
10:10=1
20:10=2
30:10=3
40:10=4
50:10=5
100:10=10
Վարժ660
60+5=65:5=13
300+5=305:5=61
4000+553=4553
5000+30=5030:5=1006
20+5=25:5=5
200+65=265:5=53
3000+257=3257
1000+20=120:5=204
Վարժ688
1×6+2×6=24
1×200+4×200=1000
24+3×2=30
300+4×300=1500
5+7×5=40
45+5×45=270
Վարժ699
6:2=3
10:2=5
15:2=3
18:2=8
20:2=10
22:2=11
30:2=15
40:2=20
50:2=250
1004:2=502
Վարժ706
3լ 450մլ = 3450մլ
42լ 50լ =4250մլ
7լ 700 մլ=7700մլ
48լ 7լ=4807մլ
մաթեմի տնային
Վարժ535
36:1=36 36:4=9 36:7=5.1 36:10=3.6 36:13=2.7
36:2=18 36:5=7.2 36:8=4.4 36:11=3.2 36:14=2.8
36:3=12 36:6=6 36:9=4 36:12=3 36:15=2.6
Վարժ538
29-4-4-4-4-4-4-4=1 38-5-5-5-5-5-5-5=3
29:4=7.1 38:5=7.3
Վարժ541
ա)լուծում՝ 1)46 մմ + 14մմ =60մմ
2)126մմ — 60մմ =66մմ
3)46մմ + 14 մմ +66 մմ =126մմ
Պատ՝66մմ
բ) լուծում՝ 1)56:2=28
2)56+12=68
Վարժ543
ա) լուծում՝
1)30:15=2
2)2×750=1500
Պատ՝ 750 դրամ
Վարժ544
ա) 5 ր 40վ > 540վ բ)7 կմ 20 մ >720մ գ)7կգ 200գ>720գ
7ժ 20 ր > 720ր 2 կմ 40մ = 2040մ 20 տ7ց>207ց
2 օր 16 ժ<216ժ 5 կմ 4 մ > 504մ 5ց78կգ<578կգ
Վարժ557
ա)15 կմ 620մ — 8 կմ 900մ=6կմ 720մ
120 մ 45 սմ- 15մ 80սմ=114 մ 65սմ
բ)24 տ 300կգ-6տ 450կգ =17տ 850կգ
Վարժ559
Կարեն- 4800 դր- 22 օր =105,600
Գոհար- 3500 դր — 25 օր =87,500
Հասմիկ- 500 դր- 20 օր = 100,000
Վարժ566
(500×2) – 1000=0
Վարժ576
․հավասար են
․հավասար են
․ ճիշտ է
․ ոչ
․ճիշտ է
Վարժ578
ա)247+153=300 բ )438+161=554
468-72=396 549-151=398
189+197+112=488 291+325+12=628
348-153+220=523 174+38-102=152
Վարժ583
ա)230-150+120=200 բ)310+220+180=710
740-160-110=470 260+260-120=400
Մաթեմ
Վարժ513
127x(426:3)-(5425:5+1296)=1845
Վարժ514
ա)a:(64×25-1576)+7041=7078
բ)302+(a-2604:6)x62=46872
Վարժ515
ա)42կմ-350մ=41կմ650մ բ)82կգ-6կգ=76կգ
12դմ25սմ -7սմ=12դմ18սմ 22տ200կգ-380կգ=21տ620կգ
գ) 25օր-15ժ=24օր9ժ
18ժ20ր-30ր=17ժ50ր
Վարժ517
Լուծում
120կմ+28կմ=148կմ
Պատ՝148կմ
Վարժ518
Լուծում
20կմ+230կմ=250կմ
Պատ՝250կմ
Վարժ519
Լուծում
75կմ-20կմ=55
Պատ`55կմ
Վարժ520
Լուծում
1)12+7+6=22
2)22×40=1000
Պատ՝1000կոճակ
Վարժ521
1)40:2=20
2)20+7=27 3)27-7=20 Պատ՝20ուլունք
Վարժ526
ա)1000-(750-250-500)=1000
5500-(570-420:6)=5000
բ)1000-(6400:32:4)=200
2010-3200:(80×4)=2000