1.Գրիր P(23;2) կետի հեռավորությունը աբսցիսների առանցքից:

P(23; 2) կետի հեռավորությունը աբսցիսների առանցքից (այսինքն՝ x-առանցքից) հավասար է այդ կետի y-կոորդինատի մոդուլին, այսինքն՝ Հեռավորությունը=∣y∣=∣2∣=2\text{Հեռավորությունը} = |y| = |2| = 2Հեռավորությունը=∣y∣=∣2∣=2

Պատասխան․ P(23; 2) կետի հեռավորությունը աբսցիսների առանցքից հավասար է 2 միավորի։

2.Գտիր հեռավորությունը G(−16;3) և N(−16;0) կետերի միջև:

Ունենք երկու կետ՝
G(−16;3)G(-16; 3)G(−16;3) և N(−16;0)N(-16; 0)N(−16;0)

Քանի որ երկու կետերն էլ ունեն նույն x=−16x = -16x=−16 աբսցիսը, նրանք գտնվում են նույն ուղղահայաց ուղղում (մեկ ուղղահայաց գծի վրա), և հեռավորությունը նրանց միջև հավասար է միայն yyy-կոորդինատների տարբերության մոդուլին։ Հեռավորությունը=∣3−0∣=∣3∣=3\text{Հեռավորությունը} = |3 — 0| = |3| = 3Հեռավորությունը=∣3−0∣=∣3∣=3

Պատասխան․ G(−16; 3) և N(−16; 0) կետերի միջև հեռավորությունը հավասար է 3 միավորի։

Պարզիրկոորդինատային հարթության վրա նշված AC հատվածի միջնակետի կոորդինատները:

4.

Պարզիր, թե կոորդինատային ո՞ր առանցքի վրա է գտնվում D(6;0) կետը և հաշվիր նրա հեռավորությունը մյուս առանցքից:

1. D(6;0) կետը գտնվում է օրդինատներիաբսցիսների

 առանցքի վրա:

2. D(6;0) կետի հեռավորությունը մյուս կոորդինատային առանցքից հավասար է 

-ի

Դիտարկենք D(6;0)D(6; 0)D(6;0) կետը:

1. Ո՞ր կոորդինատային առանցքի վրա է գտնվում:

• Քանի որ y=0y = 0y=0 է, այսինքն՝ օրդինատը 0 է, նշանակում է՝ կետը գտնվում է աբսցիսների առանցքի (այսինքն՝ x-առանցքի) վրա։

Պատասխան․ D(6;0) կետը գտնվում է աբսցիսների առանցքի վրա։

---

2. Հաշվենք նրա հեռավորությունը մյուս առանցքից (այսինքն՝ օրդինատների առանցքից, կամ y-առանցքից):

• y-առանցքը բոլոր կետերի համար ունի x=0x = 0x=0, ուստի հեռավորությունը կլինի ∣x∣=∣6∣=6|x| = |6| = 6∣x∣=∣6∣=6

Պատասխան․ D(6; 0) կետի հեռավորությունը օրդինատների առանցքից հավասար է 6 միավորի։

---

Ամբողջական պատասխան՝
D(6;0) կետը գտնվում է աբսցիսների առանցքի վրա։
D(6;0) կետի հեռավորությունը օրդինատների առանցքից հավասար է 6 միավորի։

5.Գտիր կոորդինատային հարթության վրա M(5;12) կետի հեռավորությունը կոորդինատների սկզբնակետից:

M(5; 12) կետի հեռավորությունը կոորդինատների սկզբնակետից հավասար է 13 միավորի։

1)Գրիր P(23;2) կետի հեռավորությունը աբսցիսների առանցքից:

P(23;2) կետի հեռավորությունը աբսցիսների առանցքից (x առանցքից) հավասար է կետի x-կորդինատին։

Քանի որ կետի կորդինատը P(23;2) է, դրա x-կորդինատը 23 է։ Այսպիսով, P(23;2) կետի հեռավորությունը աբսցիսների առանցքից հավասար է 23:

2)Գտիր հեռավորությունը G(−16;3) և N(−16;0) կետերի միջև

d=√√(−16−(−16))²+(3−0)²

D=√0²+3²=√9=3

Ուստի, G և N կետերի միջև հեռավորությունը 3 է։

3)

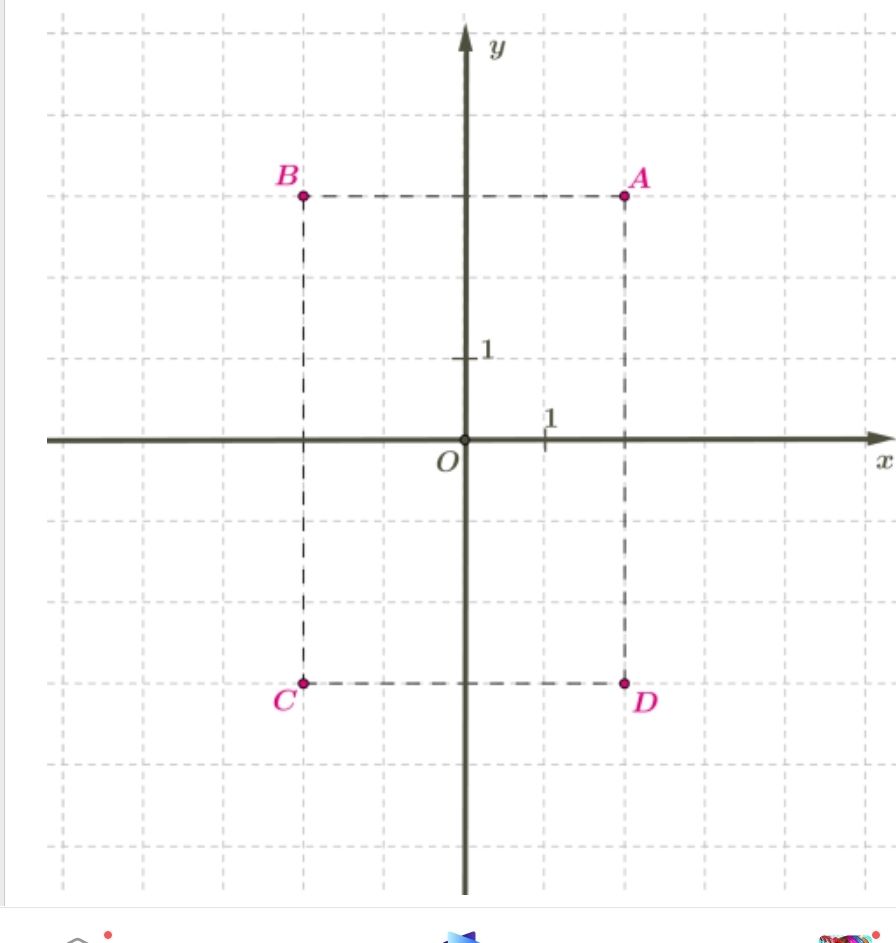
(16;14)
(8;7)

4.)Հաշվիր (16;14) կետը կոորդինատների սկզբնակետի հետ միացնող հատվածի միջնակետի կոորդինատները:

Ուստի միջնակետի կոորդինատները (8,7)-ն են:

5)

d=(x2−x1)2+(y2−y1)2
d=x2+y2
d=52+122=25+144=169=13

M(5;12)

6)Գտիր կոորդինատային հարթության վրա M(5;12) կետի հեռավորությունը կոորդինատների սկզբնակետից:

Ուստի կետի
𝑀
(
5
,
12
)
M(5,12) հեռավորությունը սկզբնակետից հավասար է 13:

7)

 A(8;1) և B(5;5)

|AB|=

2. M(5;5) և N(1;8)

|MN|=

Ուստի, ∣AB∣=5|AB| = 5∣AB∣=5:

MN∣=5:

8)

39.B, D և M կետերը գտնվում են մի ուղղի վրա: հայտնի, է BD 7 ud, MD 16 ud: որքան կարող է լինել BM հեռավորությունը:

Երբ B կետը D-ից է գտնվում:

𝐵
𝑀
=
𝐵
𝐷
−
𝑀
𝐷
=
7
−
16
=
−
9
 ud (միեւնույն է, այս տարբերակն անհնար է)
BM=BD−MD=7−16=−9 ud (միեւնույն է, այս տարբերակն անհնար է)
Երբ M կետը D-ից է գտնվում:

𝐵
𝑀
=
𝑀
𝐷
−
𝐵
𝐷
=
16
−
7
=
9
 ud
BM=MD−BD=16−7=9 ud
Երբ B և M կետերը գտնվում են նույն կողմում D-ից:

𝐵
𝑀
=
𝐵
𝐷
+
𝑀
𝐷
=
7
+
16
=
23
 ud
BM=BD+MD=7+16=23 ud
Այսպիսով, BM հեռավորությունը կարող է լինել 9 ud կամ 23 ud:

40. C կետը 64 սմ երկարությամբ AB հատվածի միջնակետն է: CA ճառագայթի վրա D կետը նշված է այնպես, որ CD — 15 սմ: Գտեք BD և DA հատվածների երկարությունները:

AB հատվածի միջնակետն է:

AB երկարությունը:

𝐴
𝐵
=
64
 սմ
AB=64 սմ
Քանի որ C կետը միջնակետ է, ապա:

𝐴
𝐶
=
𝐶
𝐵
=
𝐴
𝐵
2
=
64
2
=
32
 սմ
AC=CB=
2
AB

=
2
64

=32 սմ
CD ճառագայթի վրա D կետի հեռավորությունը:

𝐶
𝐷
=
15
 սմ
CD=15 սմ
Գտնենք DA և DB երկարությունները:

𝐴
𝐷
=
𝐴
𝐶
+
𝐶
𝐷
=
32
+
15
=
47
 սմ
AD=AC+CD=32+15=47 սմ
𝐵
𝐷
=
𝐴
𝐵
−
𝐴
𝐷
=
64
−
47
=
17
 սմ
BD=AB−AD=64−47=17 սմ
Այսպիսով, BD = 17 սմ, իսկ DA = 47 սմ:




41. 8 դմ ի հավասար MN հատվածի վրա՝ նրա C միջնակետի տարբեր կողմերում, նշված են A և B կետերն այնպես, որ CA — 7 սմ, CB — 0,24 մ Դտեք A և B հատվածների եր կարությունները՝ արտահայտված դեցիմետ րերով:

AB հատվածի միջնակետն է:

B երկարությունը:

𝐴
𝐵
=
64
 սմ
AB=64 սմ
Քանի որ C կետը միջնակետ է, ապա:

𝐴
𝐶
=
𝐶
𝐵
=
𝐴
𝐵
2
=
64
2
=
32
 սմ
AC=CB=
2
AB

=
2
64

=32 սմ
CD ճառագայթի վրա D կետի հեռավորությունը:

𝐶
𝐷
=
15
 սմ
CD=15 սմ
Գտնենք DA և DB երկարությունները:

𝐴
𝐷
=
𝐴
𝐶
+
𝐶
𝐷
=
32
+
15
=
47
 սմ
AD=AC+CD=32+15=47 սմ
𝐵
𝐷
=
𝐴
𝐵
−
𝐴
𝐷
=
64
−
47
=
17
 սմ
BD=AB−AD=64−47=17 սմ
Այսպիսով, BD = 17 սմ, իսկ DA = 47 սմ

42 20 սմ երկարություն ունեցող AB հատվածի վրա նշված է D կետը: Գտեք AD և 3D հատ վածների երկարությունները, եթե BD հատ վածը 4 սմ-ով երկար է AD հատվածից:

1. Դիտարկենք, որ AB հատվածի երկարությունը 20 սմ է:AB=AD+BDAB = AD + BDAB=AD+BD
2. Նշենք AD-ի երկարությունը xxx սմ: Այդ դեպքում BD-ի երկարությունը կլինի x+4x + 4x+4 սմ:AB=x+(x+4)AB = x + (x + 4)AB=x+(x+4)
3. Համարենք, որ AB=20AB = 20AB=20:20=x+(x+4)20 = x + (x + 4)20=x+(x+4) 20=2x+420 = 2x + 420=2x+4
4. Հանում ենք 4-ը երկու կողմերից:16=2×16 = 2×16=2x
5. Վերջում բաժանում ենք 2-ի:x=8x = 8x=8
6. Այժմ կարող ենք գտնել BD երկարությունը:BD=x+4=8+4=12BD = x + 4 = 8 + 4 = 12BD=x+4=8+4=12

Այսպիսով, AD = 8 սմ, BD = 12 սմ:

43. A, B և C կետերը արդյոք գտնվում են մի ուղղի pm, at AC-5 ud, 48-3 ud, BC-4 :

Լուծում: Եթե A, B, C կետերը գտնվեն մի ուղ ղի վրա, ապա AB, AC և BC հատված- ներից մեծը հավասար կլինի մյուս երկուսի գումարին: Ըստ պայմանի՝ ամենամեծ հատվածը՝ AC-ն, հավա սար է 5 սմ, մինչդեռ մյուս երկուսի գումարը՝ ABBC-ն, հավասար է 7 սմ: Հետևաբար՝ A, B և C կետերը մի ուղղի վրա չեն գտնվում:

Տրված տվյալներն են:

𝐴
𝐶
=
5
AC=5 ud
𝐴
𝐵
=
48
−
3
=
45
AB=48−3=45 ud
𝐵
𝐶
=
4
BC=4 ud
Եթե A, B, C կետերը գտնվում են մեկ ուղղի վրա, ապա պետք է լինի հետևյալը.

𝐴
𝐶
≤
𝐴
𝐵
+
𝐵
𝐶
AC≤AB+BC
Հաշվարկենք:

𝐴
𝐵
+
𝐵
𝐶
=
45
+
4
=
49
 ud
AB+BC=45+4=49 ud
Բայց
𝐴
𝐶
=
5
AC=5 ud:

Այստեղ
5
≤
49
5≤49 հարաբերությունը ճիշտ է, բայց մեզ պետք է նաև ապահովել, որ ամենամեծ հատվածը հավասար լինի մյուս երկուի գումարին:

Բայց իրականում,
𝐴
𝐶
AC մեծությունը չի կարող լինել մյուս հատվածների գումարը, քանի որ
𝐴
𝐵
AB և
𝐵
𝐶
BC իրենց չափերով շատ ավելի մեծ են, քան
𝐴
𝐶
AC:

Հետևաբար, A, B և C կետերը չեն կարող լինել մեկ ուղղի վրա:

A կետը գտնվում է Ox դրական կիսառանցքի, իսկ B կե- տը՝ Oy դրական կիսառանցքի վրա: Գտեք ABC եռանկյան գագաթների կոորդինատները, եթե՝ ա) OA = 5, OB = 3, p) OA = a, OB = b:

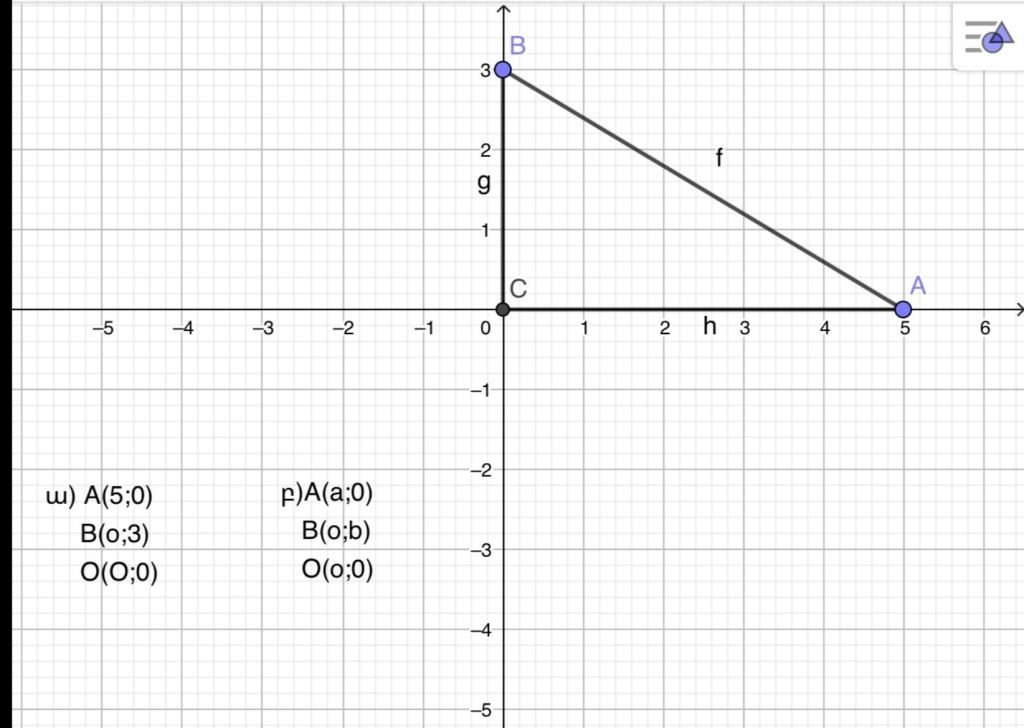
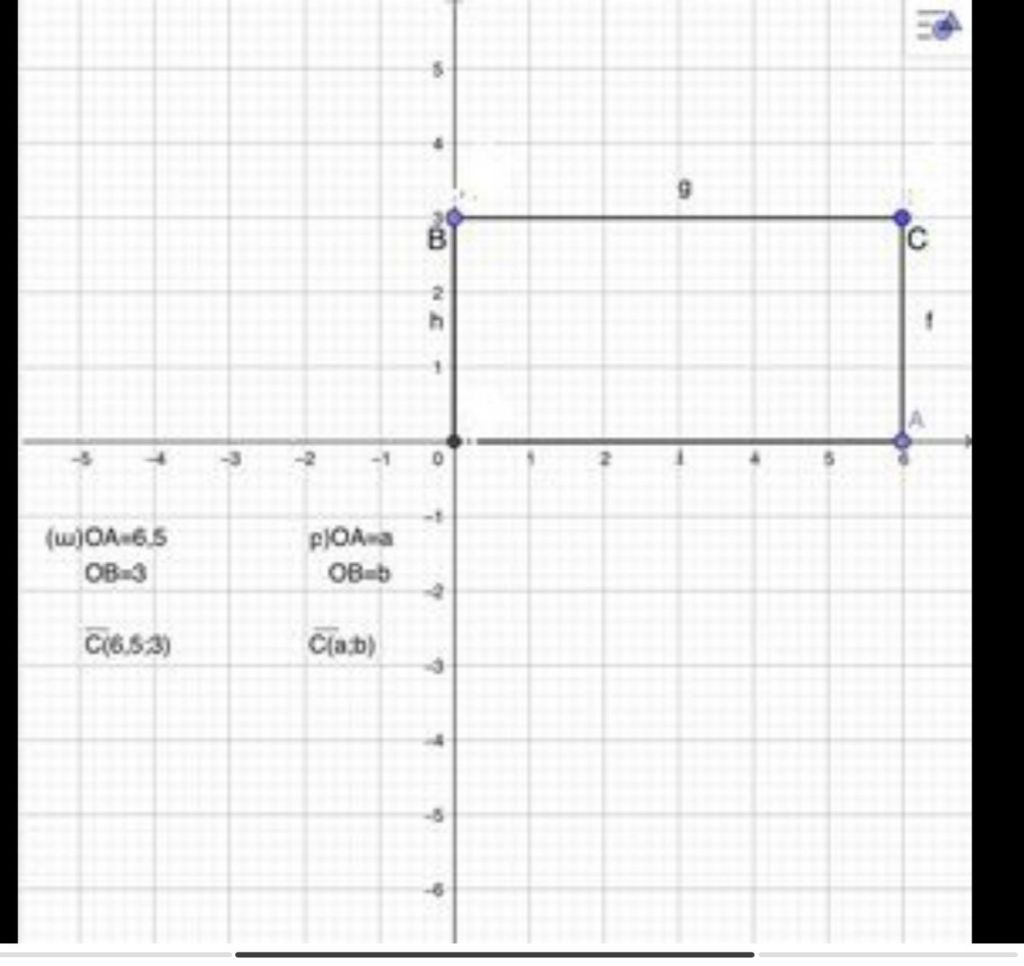
. A կետը գտնվում է Ox դրական կիսառանցքի, իսկ B կե- տը՝ Oy դրական կիսառանցքի վրա: Գտեք OACB ուղղանկ- յան գագաթների կոորդինատները, եթե՝ ա) OA = 6,5, OB=3, p) OA = a, OB = b:

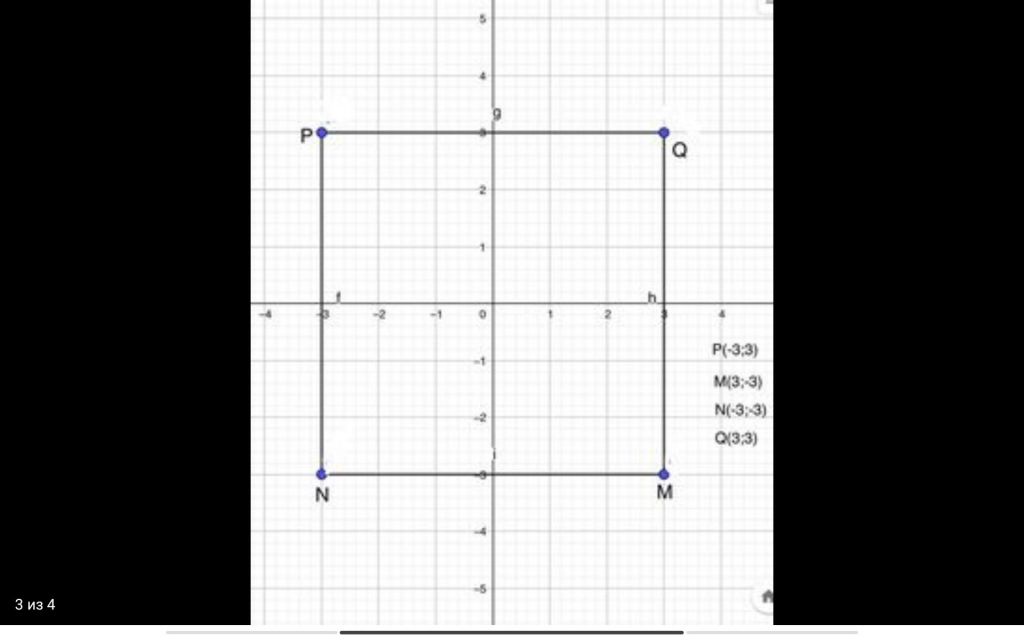
MNPQ քառակուսին գծեք այնպես, որ P գագաթն ունենա (−3, 3) կոորդինատները, իսկ անկյունագծերը հատվեն կոորդինատների սկզբնակետում։ Գտեք M. N և Q կետե- րի կոորդինատները։

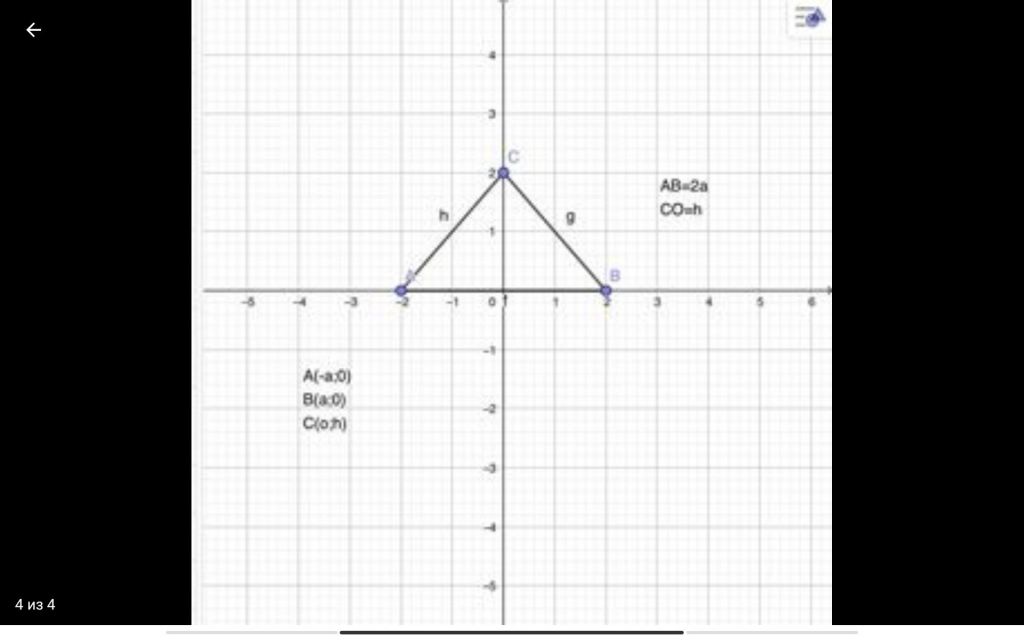
Գտեք նկար 4-ում պատկերված ABC հավասարասրուն եռանկյան գագաթների կոորդինատները, եթե AB=2a, իսկ CO բարձրությունը հավասար է հ-ի: