1)Գրիր P(23;2) կետի հեռավորությունը աբսցիսների առանցքից:
P(23;2) կետի հեռավորությունը աբսցիսների առանցքից (x առանցքից) հավասար է կետի x-կորդինատին։
Քանի որ կետի կորդինատը P(23;2) է, դրա x-կորդինատը 23 է։ Այսպիսով, P(23;2) կետի հեռավորությունը աբսցիսների առանցքից հավասար է 23:
2)Գտիր հեռավորությունը G(−16;3) և N(−16;0) կետերի միջև
d=√√(−16−(−16))²+(3−0)²
D=√0²+3²=√9=3
Ուստի, G և N կետերի միջև հեռավորությունը 3 է։
3)
(16;14)
(8;7)
4.)Հաշվիր (16;14) կետը կոորդինատների սկզբնակետի հետ միացնող հատվածի միջնակետի կոորդինատները:
Ուստի միջնակետի կոորդինատները (8,7)-ն են:
5)
d=(x2−x1)2+(y2−y1)2
d=x2+y2
d=52+122=25+144=169=13
M(5;12)
6)Գտիր կոորդինատային հարթության վրա M(5;12) կետի հեռավորությունը կոորդինատների սկզբնակետից:
Ուստի կետի
𝑀
(
5
,
12
)
M(5,12) հեռավորությունը սկզբնակետից հավասար է 13:
7)
A(8;1) և B(5;5)
|AB|=
2. M(5;5) և N(1;8)
|MN|=
Ուստի, ∣AB∣=5|AB| = 5∣AB∣=5:
MN∣=5:
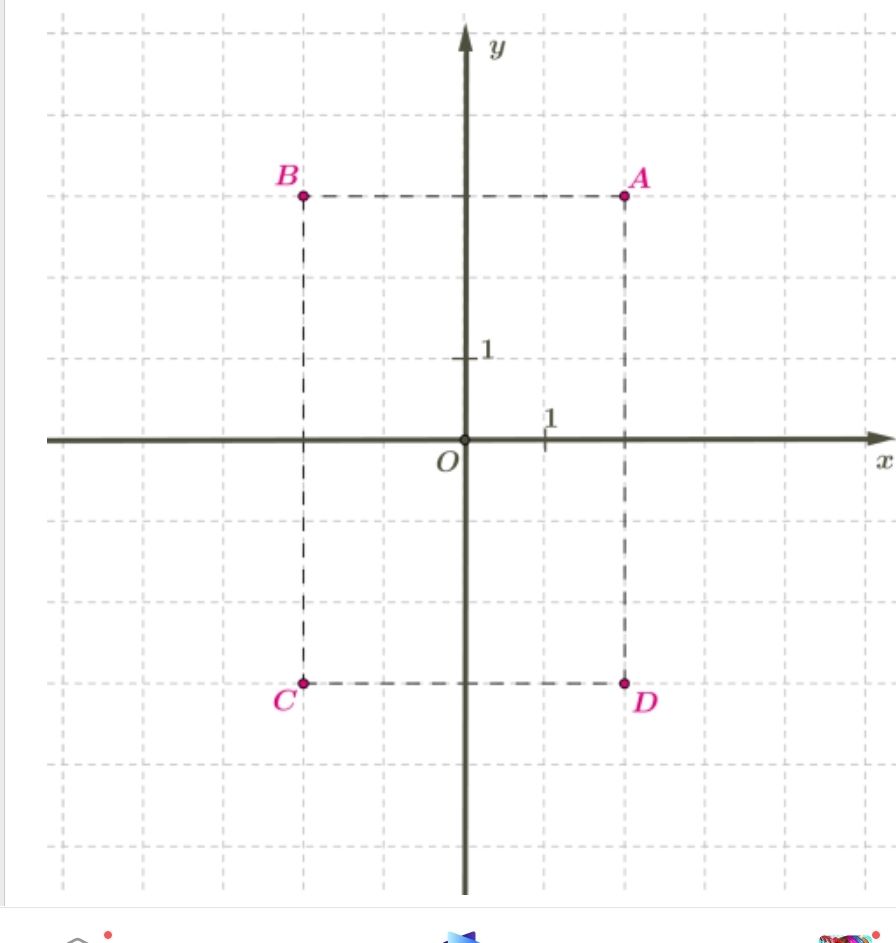
8)
Արտավազդ Մկրտչյան 10 դասարան 