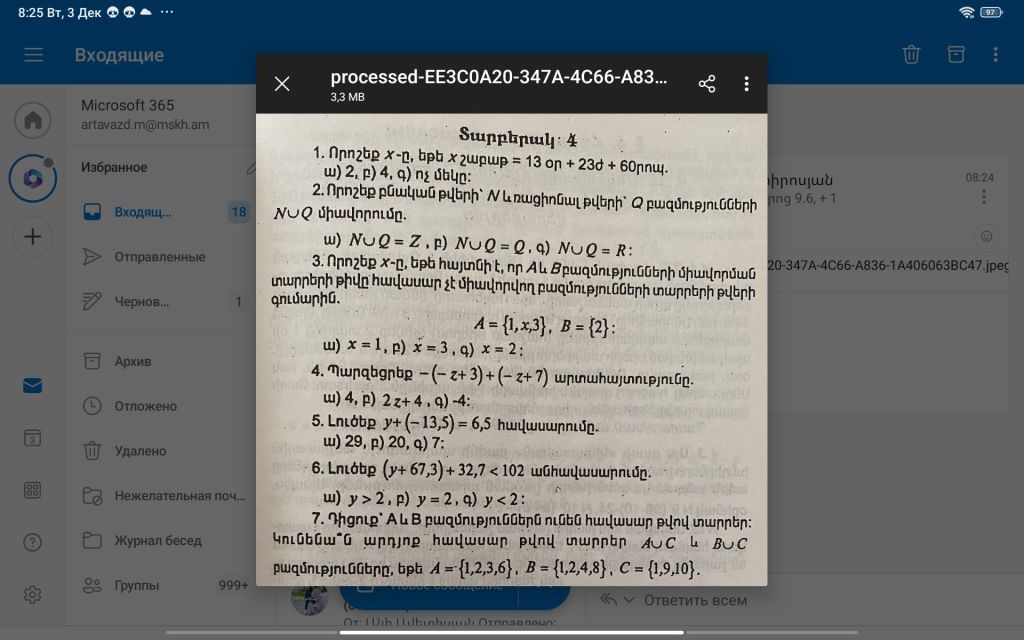
1Որոշեք x-ը, եթե x շաբաթ = 13 օր + 230 + 60րոպ ա) 2, բ) 4, գ) ոչ մեկը:
Եկեք լուծենք խնդիրը:
Մեզ տրված է, որ
𝑥
x շաբաթ = 13 օր + 230 + 60 րոպե:
Նախ, մատակարարենք, թե որքան րոպե է կազմում 1 շաբաթը:
1 շաբաթ = 7 օր, ուստի
1
շաբաթ
=
7
×
24
×
60
րոպե
=
10080
րոպե
1շաբաթ=7×24×60 րոպե=10080 րոպե
Հիմա եկեք համեմատենք տրված ժամանակահատվածը (13 օր + 230 րոպե + 60 րոպե):
13 օր =
13
×
24
×
60
=
18720
րոպե
13×24×60=18720 րոպե
230 րոպե + 60 րոպե = 290 րոպե:
Եվ այսպես, ընդհանուր ժամանակը կլինի:
18720
+
290
=
19010
րոպե
18720+290=19010 րոպե
Այժմ գտնենք
𝑥
x-ը՝ բաժանելով ստացված րոպեները 1 շաբաթվա րոպեների թվին:
𝑥
=
19010
10080
≈
1.885
x=
10080
19010
≈1.885
Քանի որ պատասխաններից ոչ մեկը չի համընկնում այս արդյունքին (2 կամ 4), ճիշտ պատասխանն է՝ գ) ոչ մեկը
2. Որոշեք բնական թվերի՝ V և ռացիոնալ թվերի՝ Q բազմությունների հng 9,6 + 1 NUQ միավորումը.
w) NUQ=Z.P) NUQ = Q.9) NUQ = R:
w)
𝑁
𝑈
𝑄
=
𝑍
NUQ=Z:
𝑍
Z-ը ամբողջ թվերի բազմությունն է, բայց մենք այստեղ չենք խոսում այդ բազմության մասին, ուստի այս տարբերակը ճիշտ չէ:
P)
𝑁
𝑈
𝑄
=
𝑄
NUQ=Q: Դա ճիշտ տարբերակն է, քանի որ
𝑉
∪
𝑄
=
𝑄
V∪Q=Q, իսկ
𝑁
𝑈
𝑄
NUQ նշանակում է
𝑉
∪
𝑄
V∪Q, այսինքն՝ ռացիոնալ թվերի բազմություն:
𝑁
𝑈
𝑄
=
𝑅
NUQ=R:
𝑅
R-ը իրական թվերի բազմությունն է, որը ընդգրկում է ռացիոնալ և անռացիոնալ թվերը, բայց դա լրացուցիչ է, այստեղ մենք միայն ռացիոնալ թվերին ենք վերաբերում, ուստի սա ճիշտ չէ:
Ճիշտ պատասխան
3. Որոշեք x-ը, եթե հայտնի է, որ A և B բազմությունների միավորման տարրերի թիվը հավասար չէ միավորվող բազմությունների տարրերի թվերի գումարին. A = {1,x,3}, B = {2}:
w) x = 1, p) x = 3,q) x = 2:
Եթե A և B բազմություններում կա ընդհանուր տարր, ապա դրանց միավորման տարրերի թիվը կլինի փոքր, քան ∣A∣+∣B∣|A| + |B|∣A∣+∣B∣:
- Եթե x=2x = 2x=2, ապա A և B բազմությունները կունենան ընդհանուր տարր՝ 2:
- Այդ դեպքում A∪B={1,2,3}A \cup B = \{1, 2, 3\}A∪B={1,2,3}, և ∣A∪B∣=3|A \cup B| = 3∣A∪B∣=3:
- Ահա այսպիսով, ∣A∪B∣=3|A \cup B| = 3∣A∪B∣=3, որը տրվում է ∣A∣+∣B∣=4|A| + |B| = 4∣A∣+∣B∣=4-ի տարբերությունից:
- Այդ դեպքում A∪B={1,2,3}A \cup B = \{1, 2, 3\}A∪B={1,2,3}, և ∣A∪B∣=3|A \cup B| = 3∣A∪B∣=3:
Այս դեպքում իրականում ∣A∪B∣≠∣A∣+∣B∣|A \cup B| \neq |A| + |B|∣A∪B∣=∣A∣+∣B∣, քանի որ 3 ≠ 4, այդպիսով լուծումն այն է, որ x=2x = 2x=2:
Պատասխան. q) x = 2.
4. Պարզեցրեք — (- z+ 3) + (- z+ 7) արտահայտությունը.
w) 4, p) 2z+4,q) -4:
Միավորենք նմանատիպ անդամները:
𝑧
−
𝑧
+
(
−
3
+
7
)
=
0
+
4
=
4
z−z+(−3+7)=0+4=4
Ուստի, արտահայտության պարզեցումը հավասար է 4:
Պատասխան՝ w) 4.
5. y+ (-13,5) = 6,5
w) 29, p) 20, q) 7:
Այժմ լուծենք
𝑦
y-ի համար. Սկզբից գումարենք 13.5 երկու կողմերից:
𝑦
=
6.5
+
13.5
y=6.5+13.5
Որպես արդյունք ստանում ենք.
𝑦
=
20
y=20
Պատասխան՝ p) 20.
6. (y+67,3) + 32,7 < 102
ш) у > 2, р) у = 2,q) y < 2:
Այժմ նվազեցնենք 100 երկու կողմերից:
𝑦
<
102
−
100
y<102−100
𝑦
<
2
y<2
Հետևաբար, պատասխանն է q) y < 2: