Երկրաչափություն մարտ

Երկրաչափություն մարտ

Երկրաչափություն 8 Ապրիլ

Երկրաչափություն 8 Ապրիլ

Երկրաչափություն 8 Ապրիլ

Երկրաչափություն 8 Ապրիլ

Երկրաչափություն 8 մայիս

Երկրաչափություն 8 մայիս

Երկրաչափություն 8 մայիս

Երկրաչափություն 8 մայիս

1.Գրել ուղանկյան,զուգահեռագծի,եռանկյան,շեղանկյան և սեղանի մակերեսների հաշվման բանաձևերը։

2.Գտնել ուղղանկյան մակերեսը,եթե դրա կողմերից մեկը մյուսից մեծ է երկու անգամ,իսկ պարագիծը հավասար է 48սմ։

3.Զուգահեռագծի կողմերն են 5սմ և 10սմ,իսկ անկյուններից մեկը 300։Գտնել զուգահեռագծի մակերեսը։

4.Գտնել 12սմ և 8սմ կողմերով ուղղանկյուն եռանկյան մակերեսը։

5.Գտնել 6սմ և 10սմ հիմքերով և 8սմ բարձրությամբ սեղանի մակերեսը։

Պատասխաններ

1. Ուղանկյան մակերեսի հաշվման բանաձևը:
   Երկարություն × Լայնություն

2. Ուղղանկյան մակերեսը:
   48 սմ²

3. Զուգահեռագծի մակերեսը:
   (5սմ + 10սմ) × 300 / 2 = 4500 սմ²

4. Ուղղանկյան եռանկյան մակերեսը:
   12սմ × 8սմ / 2 = 48 սմ²

5. Սեղանի մակերեսը:
   (6սմ × 10սմ × 8սմ) / 2 = 240 սմ²

1.

C կետը 64 սմ երկարությամբ AB հատվածի միջնակետն է: CA ճառագայթի վրա D կետը նշված է այնպես, որ CD = 15 սմ: Գտեք BD և DA հատվածների երկարությունները:
64 ։ 2=32(AC=CB)
32 + 15=47(BD)
32 — 15=17(AD)

2.

D կետը գտնվում է AB հատվածի վրա, որի երկարությունը 14 սմ է: Գտեք AD հատվածի երկարությունը, եթե DA = 3DB
Լուծում

x + 3x = 4x

4x = 14

x = 14/4

x = 3,5 սմ

14 – 3,5 = 10,5

                                                                Պատ. ՝ AD = 10,5 սմ

3.

Եռանկյան պարագիծը 48սմ է, իսկ կողմերից մեկը՝ 18սմ: Գտեք մյուս երկու կողմերը, եթե նրանց տարբերությունը 4,6սմ է:   
Տրված՝
P=48սմ

AB=18սմ

BC=x սմ

AC= x+4,6 սմ
AC,BC-?

P=AB+BC+AC
48սմ=18սմ+x+x+4,6սմ
48-18-4,6=2x
25,4սմ =2x

x=12,7
AC=4,6+12,7=17,3

4.

Հավասարասրուն եռանկյան հիմքը երկու անգամ փոքր է սրունքից, իսկ պարագիծը 50 սմ է: Գտեք եռանկյան կողմերը

Լուծում

Հավասարասրուն եռանկյան մի կողմը նշանակենք x

x + x + x/2 = 50

2x/1 + x/2 = 50

4x + x/2 = 50

5x/2 = 50/1

5x = 50 * 2

5x = 100

x = 20

AB = BC = 20

AC = x/2 = 20/2 = 10                                                  Պատ.՝ 20 սմ և 10 սմ

5.

Բութանկյուն հավասարասրուն եռանկյան պարագիծը 45 սմ է, իսկ նրա կողմերից մեկը մյուսից փոքր է 9 սմ-ով: Գտեք եռանկյան կողմերը
Լուծում

x + x + (x + 9) = 45

3x + 9 = 45

3x = 45 – 9

3x = 36

x = 36 : 3

x = 12

(x + 9) = 21                                                             Պատ.՝ 12 սմ և 21 սմ

6.

DK հիմքով DEK հավասարասրուն եռանկյան մեջ EF հատվածը կիսորդ է, DK=16 սմ, <DEF=430: Գտեք KF-ը, <DEK-ն, <EFD-ն:

<FK = 16 : 2 = 8սմ

<DEK = 43 * 2 = 86սմ

<EFD = 90^0

Պատ․՝ 8սմ, 86սմ, 90^0։

7.

Գտեք երկու ուղիղների հատումից առաջացած չփռված անկյունները, եթե՝ ա) դրանցից երկուսի գումարը 1140 է, բ) երեք անկյունների գումարը 2200 է:

<1+<2=1140

114:2=570

<3=1800-570=1230

<3=1230,<4=1230 հակադիր անկյուններ է

8. OC ճառագայթը AOB անկյունը տրոհում է եր– կու անկյան: Գտեք COB անկյունը, եթե LAOB = 78°, իսկ AOC անկյունը 18°–ով փոքր է BOC անկյունից

1.

C կետը 64 սմ երկարությամբ AB հատվածի միջնակետն է: CA ճառագայթի վրա D կետը նշված է այնպես, որ CD = 15 սմ: Գտեք BD և DA հատվածների երկարությունները:
64 ։ 2=32(AC=CB)
32 + 15=47(BD)
32 — 15=17(AD)

2.

D կետը գտնվում է AB հատվածի վրա, որի երկարությունը 14 սմ է: Գտեք AD հատվածի երկարությունը, եթե DA = 3DB
Լուծում

x + 3x = 4x

4x = 14

x = 14/4

x = 3,5 սմ

14 – 3,5 = 10,5

                                                                Պատ. ՝ AD = 10,5 սմ

3.

Եռանկյան պարագիծը 48սմ է, իսկ կողմերից մեկը՝ 18սմ: Գտեք մյուս երկու կողմերը, եթե նրանց տարբերությունը 4,6սմ է:    
Տրված՝
P=48սմ

AB=18սմ

BC=x սմ

AC= x+4,6 սմ
AC,BC-?

P=AB+BC+AC
48սմ=18սմ+x+x+4,6սմ
48-18-4,6=2x
25,4սմ =2x

x=12,7
AC=4,6+12,7=17,3

4.

Հավասարասրուն եռանկյան հիմքը երկու անգամ փոքր է սրունքից, իսկ պարագիծը 50 սմ է: Գտեք եռանկյան կողմերը

Լուծում

Հավասարասրուն եռանկյան մի կողմը նշանակենք x

x + x + x/2 = 50

2x/1 + x/2 = 50

4x + x/2 = 50

5x/2 = 50/1

5x = 50 * 2

5x = 100

x = 20

AB = BC = 20

AC = x/2 = 20/2 = 10                                                  Պատ.՝ 20 սմ և 10 սմ

5.

Բութանկյուն հավասարասրուն եռանկյան պարագիծը 45 սմ է, իսկ նրա կողմերից մեկը մյուսից փոքր է 9 սմ-ով: Գտեք եռանկյան կողմերը
Լուծում

x + x + (x + 9) = 45

3x + 9 = 45

3x = 45 – 9

3x = 36

x = 36 : 3

x = 12

(x + 9) = 21                                                             Պատ.՝ 12 սմ և 21 սմ

6.

DK հիմքով DEK հավասարասրուն եռանկյան մեջ EF հատվածը կիսորդ է, DK=16 սմ, <DEF=430: Գտեք KF-ը, <DEK-ն, <EFD-ն:

<FK = 16 : 2 = 8սմ

<DEK = 43 * 2 = 86սմ

<EFD = 90^0

Պատ․՝ 8սմ, 86սմ, 90^0։

7.

Գտեք երկու ուղիղների հատումից առաջացած չփռված անկյունները, եթե՝ ա) դրանցից երկուսի գումարը 1140 է, բ) երեք անկյունների գումարը 2200 է:

<1+<2=1140

114:2=570

<3=1800-570=1230

<3=1230,<4=1230 հակադիր անկյուններ է

8. OC ճառագայթը AOB անկյունը տրոհում է եր– կու անկյան: Գտեք COB անկյունը, եթե LAOB = 78°, իսկ AOC անկյունը 18°–ով փոքր է BOC անկյունից

1.

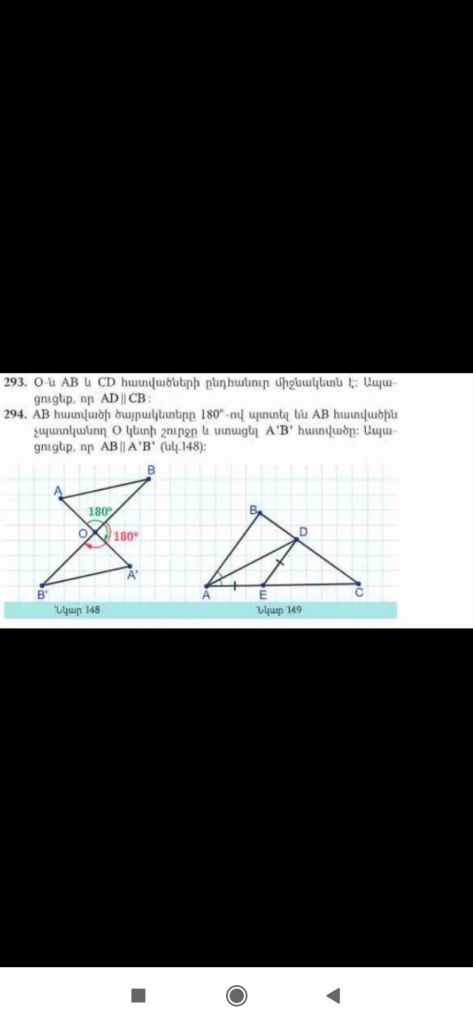
Եթե O-ն AB և CD հատվածների ընդհանուր միջնակետ է, ապա AD || CB, այնպես որ AD և CB հատվածները հատվում են միաժամանակ:

2.

ա) <1=<6։ Ապացուցեք, որ aIIb:

<1=<3 , <6=<8 , որովհետև նրանք հակադիր անկյուններ են ։Գիտենք որ <1=<6 այսինքը <3=<8 , իսկ ըստ առաջին հայտանիշի ` Եթե երկու ուղիղներ հատողով հատելիս խաչադիր անկյունները հավասար են, ապա ուղիղները զուգահեռ են ստացանք a||b

1.

C կետը 64 սմ երկարությամբ AB հատվածի միջնակետն է: CA ճառագայթի վրա D կետը նշված է այնպես, որ CD = 15 սմ: Գտեք BD և DA հատվածների երկարությունները:
64 ։ 2=32(AC=CB)
32 + 15=47(BD)
32 — 15=17(AD)

2.

D կետը գտնվում է AB հատվածի վրա, որի երկարությունը 14 սմ է: Գտեք AD հատվածի երկարությունը, եթե DA = 3DB
Լուծում

x + 3x = 4x

4x = 14

x = 14/4

x = 3,5 սմ

14 – 3,5 = 10,5

                                                                Պատ. ՝ AD = 10,5 սմ

3.

Եռանկյան պարագիծը 48սմ է, իսկ կողմերից մեկը՝ 18սմ: Գտեք մյուս երկու կողմերը, եթե նրանց տարբերությունը 4,6սմ է: 
Տրված՝
P=48սմ

AB=18սմ

BC=x սմ

AC= x+4,6 սմ
AC,BC-?

P=AB+BC+AC
48սմ=18սմ+x+x+4,6սմ
48-18-4,6=2x
25,4սմ =2x

x=12,7
AC=4,6+12,7=17,3

4.

Հավասարասրուն եռանկյան հիմքը երկու անգամ փոքր է սրունքից, իսկ պարագիծը 50 սմ է: Գտեք եռանկյան կողմերը

Լուծում

Հավասարասրուն եռանկյան մի կողմը նշանակենք x

x + x + x/2 = 50

2x/1 + x/2 = 50

4x + x/2 = 50

5x/2 = 50/1

5x = 50 * 2

5x = 100

x = 20

AB = BC = 20

AC = x/2 = 20/2 = 10                                                  Պատ.՝ 20 սմ և 10 սմ

5.

Բութանկյուն հավասարասրուն եռանկյան պարագիծը 45 սմ է, իսկ նրա կողմերից մեկը մյուսից փոքր է 9 սմ-ով: Գտեք եռանկյան կողմերը
Լուծում

x + x + (x + 9) = 45

3x + 9 = 45

3x = 45 – 9

3x = 36

x = 36 : 3

x = 12

(x + 9) = 21                                                             Պատ.՝ 12 սմ և 21 սմ

6.

DK հիմքով DEK հավասարասրուն եռանկյան մեջ EF հատվածը կիսորդ է, DK=16 սմ, <DEF=430: Գտեք KF-ը, <DEK-ն, <EFD-ն:

<FK = 16 : 2 = 8սմ

<DEK = 43 * 2 = 86սմ

<EFD = 90^0

Պատ․՝ 8սմ, 86սմ, 90^0։

7.

Գտեք երկու ուղիղների հատումից առաջացած չփռված անկյունները, եթե՝ ա) դրանցից երկուսի գումարը 1140 է, բ) երեք անկյունների գումարը 2200 է:

<1+<2=1140

114:2=570

<3=1800-570=1230

<3=1230,<4=1230 հակադիր անկյուններ է

8. OC ճառագայթը AOB անկյունը տրոհում է եր– կու անկյան: Գտեք COB անկյունը, եթե LAOB = 78°, իսկ AOC անկյունը 18°–ով փոքր է BOC անկյունից

130.

Երեք կետերը չեն գտնվում մի ուղ-ղի վրա, եթե դրանք անցնում են որևէ շրջանագծի միջոցով կետերից մեկի։ Այդ դեպքում հաջորդ երկու կետերը չեն կրկնվում ու չեն հանվում եղած ուղ-ղի վրա:

131.

Երեք կետերի անցման միջոցով հատվածը անվանում ենք «երեք կետի անցումով հատված»։ Այսպես, երբ կան երեք կետեր, որոնք երկու հատվածներ անցնում են հատվածով, ապա այդ միջոցով հատվածի անցումն ավարտվում է մեկ կետում։

132.

Ա) Երբ չորս կետերով անցնող շրջանա-գիծը ունի գոյություն, ապա այն կոչվում է զանազան շրջանագծերի շեղման կետ։

Բ) Երբ չորս կետերով անցնող շրջանա-գիծը չունի գոյություն, ապա այն կոչվում է ծայրակետ շրջանագծ։

143.

Քանի որ բոլոր շառավիղերը հավասար են DO=AD=16:2=8 Անկյունները հավասար են ը այդ անկյունը կազմող կողմերը իրար հավասար են քանի որ շրջանագիծ է 8+8+13=29

144.


BO=OA=OC որովհետև բոլորը շրռավիղեր են , ըստ պայմանի BC=CA , BOC եռանկյունը հավասարասրուն է իսկ դա նշանակում է որ <4=<3 իսկ AOC-ում <1=<2 , իսկ BAC եռանկյունը ըստ պայմանի հավասարասրուն է իսկ հավասարասրուն եռանկյան հիմքին կից անկյունները հավասար են այպիսով <4=<1: <B=x <A=x <C=2x 180:4=45 x=45 իսկ դա նշանակում է որ A=C=45 180-45*2=90
<AOC=90

Պատ․՝ուղիղ անկյուն

145.

Շրջանագծի A կետով տարված են շոշափող և շառավիղին հավասար լար: Գտեք դրանց կազմած անկյունը:

Ստացվում է հավասարասրուն եռանկյուն հետևաբար 180:3=60

3) AB ուղիղը B կետում շոշափում է O կենտրոնով և r=1,5սմ շառավիղով շրջանը: Գտեք ABO եռանկյան անկյունները, եթե AO=3սմ:

ըստ քառանկյուն-երանկյան հայտանիշի <A=30 <B=90 180-(30+90)=60

1.

C կետը 64 սմ երկարությամբ AB հատվածի միջնակետն է: CA ճառագայթի վրա D կետը նշված է այնպես, որ CD = 15 սմ: Գտեք BD և DA հատվածների երկարությունները:
64 ։ 2=32(AC=CB)
32 + 15=47(BD)
32 — 15=17(AD)

2.

D կետը գտնվում է AB հատվածի վրա, որի երկարությունը 14 սմ է: Գտեք AD հատվածի երկարությունը, եթե DA = 3DB
Լուծում

x + 3x = 4x

4x = 14

x = 14/4

x = 3,5 սմ

14 – 3,5 = 10,5

                                                                Պատ. ՝ AD = 10,5 սմ

3.

Եռանկյան պարագիծը 48սմ է, իսկ կողմերից մեկը՝ 18սմ: Գտեք մյուս երկու կողմերը, եթե նրանց տարբերությունը 4,6սմ է: 
Տրված՝
P=48սմ

AB=18սմ

BC=x սմ

AC= x+4,6 սմ
AC,BC-?

P=AB+BC+AC
48սմ=18սմ+x+x+4,6սմ
48-18-4,6=2x
25,4սմ =2x

x=12,7
AC=4,6+12,7=17,3

4.

Հավասարասրուն եռանկյան հիմքը երկու անգամ փոքր է սրունքից, իսկ պարագիծը 50 սմ է: Գտեք եռանկյան կողմերը

Լուծում

Հավասարասրուն եռանկյան մի կողմը նշանակենք x

x + x + x/2 = 50

2x/1 + x/2 = 50

4x + x/2 = 50

5x/2 = 50/1

5x = 50 * 2

5x = 100

x = 20

AB = BC = 20

AC = x/2 = 20/2 = 10                                                  Պատ.՝ 20 սմ և 10 սմ

5.

Բութանկյուն հավասարասրուն եռանկյան պարագիծը 45 սմ է, իսկ նրա կողմերից մեկը մյուսից փոքր է 9 սմ-ով: Գտեք եռանկյան կողմերը
Լուծում

x + x + (x + 9) = 45

3x + 9 = 45

3x = 45 – 9

3x = 36

x = 36 : 3

x = 12

(x + 9) = 21                                                             Պատ.՝ 12 սմ և 21 սմ

6.

DK հիմքով DEK հավասարասրուն եռանկյան մեջ EF հատվածը կիսորդ է, DK=16 սմ, <DEF=430: Գտեք KF-ը, <DEK-ն, <EFD-ն:

<FK = 16 : 2 = 8սմ

<DEK = 43 * 2 = 86սմ

<EFD = 90^0

Պատ․՝ 8սմ, 86սմ, 90^0։

7.

Գտեք երկու ուղիղների հատումից առաջացած չփռված անկյունները, եթե՝ ա) դրանցից երկուսի գումարը 1140 է, բ) երեք անկյունների գումարը 2200 է:

<1+<2=1140

114:2=570

<3=1800-570=1230

<3=1230,<4=1230 հակադիր անկյուններ է

205.

Եռանկյան ներգծյալը կարող եք գտնել այսպես՝

1. Հաշվեք եռանկյան մակերեսը: Եթե եռանկյան երկարությունը էջերի գումարից մեծ է, ապա կարելի է ներգծյալը հաշվել երկարությամբ՝ երկարությամբ՝ \( \frac{{17}}{{2}} — 13 \).
 
2. Եթե եռանկյան երկարությունը էջերի գումարից փոքր է, ապա կարելի է ներգծյալը հաշվել երկարությամբ՝ \( 13 — \frac{{17}}{{2}} \).

Հաշվելուց հետո կարող եք արդյոք կազմած շրջանագծի շառավիղը:

206.

Եռանկյան ներգծյալ շրջանագծի շառավիղը կարող եք գտնել հետևյալ բանաձևով՝ եռանկյան պարագիծի կետերի քառակուսի քառակուսի գումարը բաժանելով 4-ի: Եթե եռանկյան պարագիծը հավասար է 36 սմ, ապա բաժանված քառակուսի գումարը՝ \( \frac{36}{4} = 9 \) սմ է: Դրանից հետո, ըստ Տրդեփեանի թեորեմը, եռանկյան ներքնաձիգը՝ 15 սմ է, այնպես որ դրանից հետո եռանկյան շրջանագծի շառավիղը՝ \(15 — 9 = 6\) սմ է։

207.

Եռանկյունի ABC երկարությունը O-նից ներքին գծի եզրափակիչ կետն է: Կենտրոնները կգտնվեն երկու կետի գծային հավասարումից: Եթե ∠ABC-ն 80° է, ապա ∠AOC-ն կլինի չափի 80% կետից O-ին գալիս, որտեղ C է ABC եռանկյան կենտրոնը: Դրանից հետո, ∠AOC-ն կլինի 80° * 0.8 = 64°: